Преди няколко години астрономът Джералд С. Хокинс, вече пенсиониран от Бостънския университет, за­белязал, че някои от най-поразителните фигури на жит­ните кръгове въплъщават геометрични теореми, изразя­ващи нумерологични взаимовръзки между отделните кръгове, триъгълници и други фигури, съставящи кон­фигурациите.

Хокинс установил, че може да използва законите на Евклидовата геометрия, за да докаже четири теореми, изведени от взаимовръзките между пространствата, изобразени в тези фигури. Освен това открил пета, по-обща теорема [негова], от която можел да изведе оста­налите четири.

Любопитното е, че Хокинс не могъл да намери отпратки на тази теорема в работата на Евклид или в другите трудове, с които се консултирал. Когато предиз­викал читателите на "Сайънс Нюз" и "Математикс Тий-чър" да изведат неговата непубликувана теорема от че­тирите варианта, никой не постигнал успех.

Миналото лято, обаче, "творците на житните кръго­ве показаха познаване на петата теорема", обяснява Хо­кинс. Сред десетките кръгове, очертани внимателно в житните ниви в Англия, поне една фигура отговаря на теоремата на Хокинс.

Хората, отговорни за тази старомодна математи­ческа находчивост, остават общо взето неизвестни. Тех­ните творения пренебрегват удобствата на Евклидова геометрия и издават удивителна способност за неулови­мо проникване в нивите, огъвайки стъблата на растени­ята, без да пречупят нито един клас, и очертавайки сложни, прецизни фигури, с помощта на най-обикновени пръчки и въжета, под прикритието на мрака.

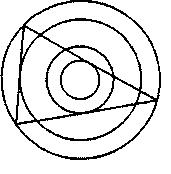
Петата теорема на Хокинс за житните кръгове включва триъгълник и различни концентрични кръгове, които се допират до стените и ъглите на триъгълника ... равностранният триъгълник образува една от наблюда­ваните в житните кръгове фигури: три равнобедрени триъгълника образуват другите геометрични фигури в житните кръгове.